1886. Determine Whether Matrix Can Be Obtained By Rotation

Problem

Given two n x n binary matrices mat and target, return true if it is possible to make mat equal to target by rotating mat in 90-degree increments, or false otherwise.

Example 1:

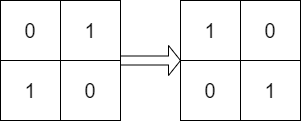
Input: mat = [[0,1],[1,0]], target = [[1,0],[0,1]]
Output: true
Explanation: We can rotate mat 90 degrees clockwise to make mat equal target.

Example 2:

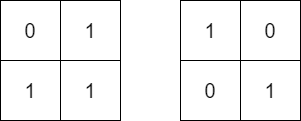
Input: mat = [[0,1],[1,1]], target = [[1,0],[0,1]]
Output: false
Explanation: It is impossible to make mat equal to target by rotating mat.

Example 3:

Input: mat = [[0,0,0],[0,1,0],[1,1,1]], target = [[1,1,1],[0,1,0],[0,0,0]]
Output: true
Explanation: We can rotate mat 90 degrees clockwise two times to make mat equal target.

Constraints:

• n == mat.length == target.length
• n == mat[i].length == target[i].length
• 1 <= n <= 10
• mat[i][j] and target[i][j] are either 0 or 1.

Concept

The problem utilizes the formula for n x n matrix rotation. This isn’t to be confused with rotation matrices in computer graphics.
The idea goes that to rotate a matrix, we need to shift the element at i, j to n-j-1, i where n is the number of rows of column. This formula only works on n x n matrices.

Formula

tempmatrix[n-j-1] = matrix[i][j]

Solution

There are only 3 possible rotations to check, as the 4th rotation is the matrix itself. So we rotate once and compare the rotated matrix with the target for match. If there s no match, try next rotation.

Algorithm

1. Compare given matrix with target without any rotations.
   1. If matched, return true.
   2. else continue.
2. Initialize a temporary matrix to store the rotated matrix.
3. Repeat 3 times:
   1. Apply rotation.
   2. Compare rotated matrix to target.
      1. If matched, return true.
      2. else continue.
   3. Replace original matrix with rotated matrix.
4. If none of the rotations match, return false.

Complexity

Time	Space
O(n²)	O(n²)

Implementation

bool compare(int** temp, int** target, int matSize) {
    for (int i = 0; i < matSize; i++)
        for (int j = 0; j < matSize; j++)
            if (target[i][j] != temp[i][j])
                return false;
    return true;
}
 
void copy(int** temp, int** mat, int matSize) {
    for (int i = 0; i < matSize; i++)
        for (int j = 0; j < matSize; j++)
            mat[i][j] = temp[i][j];
}
 
bool findRotation(int** mat, int matSize, int* matColSize, int** target, int targetSize, int* targetColSize) {
 
    if (compare(mat, target, matSize))
            return 1;
           
    int** tempmat = (int**)malloc(matSize * sizeof(int*)); // Allocate rows
    for (int i = 0; i < matSize; i++)
        tempmat[i] = (int*)malloc(matSize * sizeof(int)); // Allocate columns
 
    for (int i = 1; i <= 3; i++) {
        for (int i = 0; i < matSize; i++)
            for (int j = 0; j < matSize; j++)
                tempmat[matSize - j - 1][i] = mat[i][j];
 
        if (compare(tempmat, target, matSize))
            return 1;
 
        copy(tempmat, mat, matSize);
    }
    
    return 0;
}